サインカーブ
サインカーブで通常の直線逓減や曲線逓減とはちょっと異なる緩和曲線を作る場合の各種数値を紹介します。曲率の変化がサインの4分の1波長となる曲線の、模型向けの代用とも表現できる曲線になっています。ここではサインカーブ(サイン四半波長逓減曲線)と書きます。
サイン曲線の各種微分と曲率 \(\kappa\) などの数値は以下のようになります。
\[\begin{align} y &= A \sin kx \\ y' &= Ak \cos kx \\ y'' &= - Ak^2 \sin kx \\ \kappa &= \frac{y''}{|v|^3} = - \frac{Ak^2 \sin kx }{ |v|^3} \\ |v| &= \sqrt{ 1 + (y')^2 } = \sqrt{ 1 + A^2k^2 \cos^2 kx } \end{align}\]緩和曲線長 \(X\) は、\(kx = \frac{\pi}{2}\) となる \(x\) なので、その時の曲率は
\[\begin{align} \frac{1}{R} = -\kappa_X = Ak^2 \tag{1}\\ \end{align}\]緩和曲線全体でで曲がる角度\(\Theta\) は、
\[\begin{align} \tan\Theta = \left. y'\right|_{x=0} = Ak \tag{2} \\ \end{align}\](2)を(1)で割って、
\[\begin{align} \frac{1}{k} = R\tan\Theta \tag{3}\\ \end{align}\](1)を変形して(3)を代入して、
\[\begin{align} A = \frac{1}{k^2R} = R\tan^2\Theta \tag{4}\\ \end{align}\]これら\(\Theta\)を使った表式で書くと、
\[\begin{align} y = R\tan^2\Theta \sin \frac{x}{R\tan\Theta}\\ \end{align}\]となります。また緩和曲線長\(X\)は、
\[\begin{align} X = \frac{\pi}{2k} \\ k = \frac{\pi}{2X} \\ \end{align}\]と書けるので(3)を変形して代入し、
\[ \tan\Theta = \frac{1}{kR} = \frac{2X}{\pi R} \\ \](4)に代入して、
\[ A = \frac{4X^2}{\pi^2R} \\ \]これら\(X\)を使った表式で書くと、
\[\begin{align} y = \frac{4X^2}{\pi^2R} \sin \frac{x}{2X}\pi\\ \end{align}\]緩和曲線として適切かどうかは\(\kappa\)のグラフの形状を調べます。まず、\(\kappa\)が上に凸であってほしいので、変曲点があるか調べます。なお、
\[\begin{align} %dl &= \sqrt{dx^2 +dy^2} \\ \frac{dl}{dx} &= \sqrt{1 + (y')^2} = |v| \\ \end{align}\]です。\(\frac{d\kappa}{dl}\)は、
\[\begin{align} \frac{d\kappa}{dl} &= \frac{dx}{dl}\frac{d\kappa}{dx} \\ %&= \frac{y''}{|v|^3} &= \frac{1}{|v|} \frac{y'''|v|^3 - 3y''|v|^2(|v|)'}{|v|^6} \\ &= \frac{y'''|v|^2 - 3y''|v|(|v|)'}{|v|^6} \\ \end{align}\]また、
\[\begin{align} (|v|)' = \frac{y' y''}{\sqrt{ 1 + (y')^2 }} = \frac{y' y''}{|v|} \\ \end{align}\] \[\begin{align} |v|(|v|)' = y' y'' \\ \end{align}\]なので、
\[\begin{align} \frac{d\kappa}{dl} &= \frac{y'''(1+(y')^2) - 3y'(y'')^2}{|v|^6} \\ &= \frac{y'''+y'''(y')^2 - 3y'(y'')^2}{|v|^6} \\ % &= \frac{-Ak^3 \cos kx -Ak^3 \cos kx A^2k^2 \cos^2 kx - 3Ak \cos kx A^2k^4 \sin^2 kx}{|v|^6} \\ &= \frac{-Ak^3 \cos kx -A^3k^5 \cos^3 kx - 3A^3k^5 \cos kx \sin^2 kx}{|v|^6} \\ % &= -Ak^3 \cos kx\frac{1 +A^2k^2 \cos^2 kx + 3A^2k^2 \sin^2 kx}{|v|^6} \\ &= -Ak^3 \cos kx\frac{2 + 2A^2k^2 \sin^2 kx}{|v|^6} \\ &= -2Ak^3 \cos kx\frac{1 + A^2k^2 \sin^2 kx}{|v|^6} \\ %&= -\frac{2Ak^3 \cos kx}{|v|^4 } \\ \end{align}\]\(\frac{d^2\kappa}{dl^2}\)は、
\[\begin{align} \frac{d^2\kappa}{dl^2} &= \frac{dx}{dl}\frac{d}{dx}\left(\frac{d\kappa}{dl}\right) \\ % &= -\frac{2Ak^3}{|v|^{9}} \left[ ( -k\sin kx |v|^{4} - 4\cos kx |v|^3(|v|)' \right] \\ % &= -\frac{2Ak^3}{|v|^{7}} \left[ ( -k\sin kx |v|^{2} - 4\cos kx |v|(|v|)' \right] \\ % &= -\frac{2Ak^3}{|v|^{7}} \left[ ( -k\sin kx (1+(y')^2) - 4\cos kx y'y'' \right] \\ % &= -\frac{2Ak^3}{|v|^{7}} \left[ ( -k\sin kx (1+ A^2k^2 \sin^2 kx ) + 4\cos kx Ak\sin kx Ak^2\cos kx \right] \\ % &= -\frac{2Ak^3}{|v|^{13}} \big[ % ( -k\sin kx (1+ A^2k^2 \sin^2 kx ) % + \cos kx 2A^2k^3 \sin kx \cos kx ) |v|^{6} % - \cos kx (1+ A^2k^2 \sin^2 kx ) 6|v|^{5}(|v|)' % \big] \\ &= -\frac{2Ak^3}{|v|^{13}} \Big[ \big( -k\sin kx (1+ A^2k^2 \sin^2 kx ) + 2A^2k^3 \sin kx \cos^2 kx \big) |v|^{6} \\ &\qquad\qquad - 6\cos kx (1+ A^2k^2 \sin^2 kx ) |v|^{5}(|v|)' \Big] \\ &= -\frac{2Ak^3}{|v|^{9}} \Big[ \big( -k\sin kx (1+ A^2k^2 \sin^2 kx ) + 2A^2k^3 \sin kx \cos^2 kx ) |v|^{2} \\ &\qquad\qquad - 6\cos kx (1+ A^2k^2 \sin^2 kx ) y'y'' \Big] \\ % &= -\frac{2Ak^3}{|v|^{9}} \left[ % ( -k\sin kx (1+ A^2k^2 \sin^2 kx ) % + 2A^2k^3 \sin kx \cos^2 kx ) %(1+ A^2k^2 \cos^2 kx ) % - 6\cos kx (1+ A^2k^2 \sin^2 kx ) %(-A^2k^3 \cos kx \sin kx) % \right] \\ &= -\frac{2Ak^3}{|v|^{9}} \Big[ \big( -k\sin kx (1+ A^2k^2 \sin^2 kx ) + 2A^2k^3 \sin kx \cos^2 kx \big) (1+ A^2k^2 \cos^2 kx ) \\ &\qquad\qquad + 6A^2k^3 \cos^2 kx \sin kx (1+ A^2k^2 \sin^2 kx ) \Big] \\ &= \frac{2Ak^4}{|v|^{9}} \sin kx \Big[ \big( 1+ A^2k^2 \sin^2 kx - 2A^2k^2 \cos^2 kx \big) (1+ A^2k^2 \cos^2 kx ) \\ &\qquad\qquad - 6A^2k^2 \cos^2 kx (1+ A^2k^2 \sin^2 kx ) \Big] \\ &= \frac{2Ak^4}{|v|^{9}} \sin kx \big[ ( 1+ A^2k^2 -3A^2k^2 \cos^2 kx ) (1+ A^2k^2 \cos^2 kx ) \\ &\qquad\qquad - 6A^2k^2 \cos^2 kx (1+ A^2k^2 - A^2k^2 \cos^2 kx ) \big] \\ % &= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ %( 1+ A^2k^2 -3A^2k^2 \cos^2 kx ) % + A^2k^2 \cos^2 kx % ( 1+ A^2k^2 -3A^2k^2 \cos^2 kx ) % - 6A^2k^2 \cos^2 kx (1+ A^2k^2 - A^2k^2 \cos^2 kx ) % \right] \\ % &= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ % ( 1+ A^2k^2 -3A^2k^2 \cos^2 kx ) % + A^2k^2 \cos^2 kx % ( -5 -5A^2k^2 +3 A^2k^2 \cos^2 kx ) % \right] \\ % &= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ % 1+ A^2k^2 -3A^2k^2 \cos^2 kx % -5 A^2k^2 \cos^2 kx % -5 A^4k^4 \cos^2 kx % +3 A^4k^4 \cos^4 kx % \right] \\ % &= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ % 1+ A^2k^2 -8 A^2k^2 \cos^2 kx %-5 A^4k^4 \cos^2 kx % +3 A^4k^4 \cos^4 kx %\right] \\ %&= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ % 1+ A^2k^2 - A^2k^2 (8+5A^2k^2) \cos^2 kx %+3 A^4k^4 \cos^4 kx % \right] \\ %&= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ % 1+ A^2k^2 % +3 A^4k^4 \left( \cos^4 kx -\frac{8+5A^2k^2}{3 %A^2k^2} \cos^2 kx \right) % \right] \\ %&= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ % 1+ A^2k^2 % +3 A^4k^4 \left[ \left( \cos^2 kx -%\frac{8+5A^2k^2}{6 A^2k^2} \right)^2 % - \left( \frac{8+5A^2k^2}{6 A^2k^2} \right)^2 % \right] % \right] \\ %&= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ % 1+ A^2k^2 % +3 A^4k^4 \left( \cos^2 kx -\frac{8+5A^2k^2}{6 %A^2k^2} \right)^2 % - \frac{(8+5A^2k^2)^2}{12} % \right] \\ %&= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ % 1+ A^2k^2 % +3 A^4k^4 \left( \cos^2 kx -\frac{8+5A^2k^2}{6 %A^2k^2} \right)^2 % - \frac{64+80A^2k^2+25A^4k^4}{12} % \right] \\ %&= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ % 3 A^4k^4 \left( \cos^2 kx -\frac{8+5A^2k^2}{6 %A^2k^2} \right)^2 %2 + \frac{-52-68A^2k^2-25A^4k^4}{12} % \right] \\ %&= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ % 1+ A^2k^2 -8 A^2k^2 \cos^2 kx %-5 A^4k^4 \cos^2 kx % +3 A^4k^4 \cos^4 kx % \right] \\ %&= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ % A^4k^4 (3\cos^4 kx -5 \cos^2 kx ) % +A^2k^2 (1- 8\cos^2 kx ) + 1 %\right] \\ &= \frac{2Ak^4}{|v|^{9}} \sin kx \left[ A^4k^4 \cos^2kx (3\cos^2 kx -5 ) +A^2k^2 (1- 8\cos^2 kx ) + 1 \right] \\ % &= \frac{2Ak^4}{|v|^{7}} \sin kx \left[ 1+ A^2k^2 \sin^2 kx - 4A^2k^2\cos^2 kx \right] \\ % &= \frac{2Ak^4}{|v|^{7}} \sin kx \left[ 1+ A^2k^2 - 5A^2k^2\cos^2 kx \right] \\ % &= \frac{2Ak^4}{|v|^{7}} \sin kx \left[ 1+ A^2k^2 ( 1 - 5\cos^2 kx ) \right] \\ \end{align}\]\(\frac{d^2\kappa}{dl^2} =0 \)となるのは、以下のときです。
\[\begin{align} A^4k^4 \cos^2kx (3\cos^2 kx -5 ) +A^2k^2 (1- 8\cos^2 kx ) + 1 =0 \tag{5} \end{align}\]\(x \gt 0\)で\(\kappa\)が変曲点を持つ場合、\(x \gt 0\)で\(\frac{d^2\kappa}{dl^2} =0 \)となります。\(x \gt 0\)で変曲点を持つような\(A^2k^2\)と変曲点を持たないような\(A^2k^2\)の境は、\(x=0\)で\(\frac{d^2\kappa}{dl^2} =0 \)となるような\(A^2k^2\)なので、そのような\(A^2k^2\)は\(x=0\)で\(\frac{d^2\kappa}{dl^2} =0 \)となる\(A^2k^2\)です。\(x=0\)のとき(5)は、
\[\begin{align} A^4k^4 (3 -5 ) +A^2k^2 (1- 8 ) + 1 =0 \\ 2 A^4k^4 +7A^2k^2 -1 =0 \\ \end{align}\]となります。2次方程式解の公式を使って、求めたい\(A^2k^2\)は、
\[ A^2k^2 %= \frac{-7\pm\sqrt{49+8}}{4} \\ = \frac{-7+\sqrt{57}}{4} \\ \]このときの\(\Theta\)は、
\[ \tan\Theta = Ak = \frac{\sqrt{-7+\sqrt{57}}}{2} \] \[ \Theta = 20.3425... \]このときの\(X\)と\(R\)の比は、
\[\begin{align} \frac{X}{R} &= \frac{\pi}{2}\tan\Theta \\ &=\frac{\sqrt{-7+\sqrt{57}}}{4}\pi \\ & = 0.582537... \\ \end{align}\]\(\frac{d\kappa}{dl}\)のグラフは、\(A^2k^2\)を変えると以下のようなグラフになります。
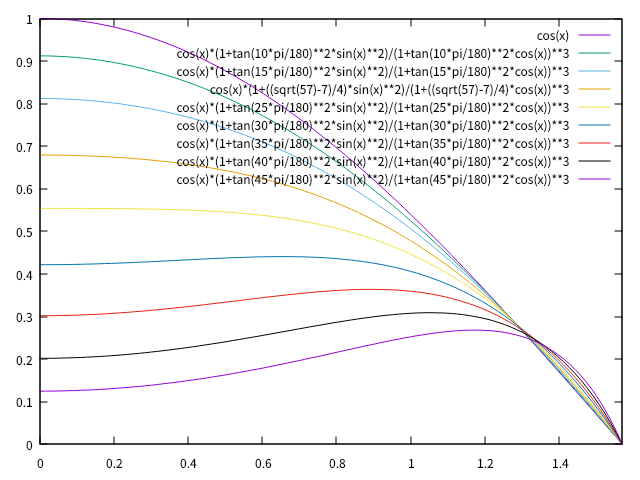
変曲点が存在しない範囲では、サイン曲線四半波長の曲率は、直線と繋がる部分は斜めに角折れがあり、円曲線と繋がる部分は折れることなく接続されます。
直線と接続する部分が斜めで角折れがあり、円曲線と接続する部分の近くが曲線になって角折れがない形状なので、曲率の実際の形状がサインの四半波長の形状に近いかそうでないかは、変曲点がない範囲ではあまり重要なことではないでしょう。使用できる角度が 20.34... [deg] までと模型でも使いやすい範囲なので、計算も含めて便利な曲線でしょう。
また変曲点がない場合では、サイン曲線は全緩和曲線(間に円曲線がない)にも向いていて、間の円曲線の長さが短い場合にも適用でいる曲線となります。
鉄道模型で半径が無限大にならない曲線(楕円、円などに線を巻き付ける曲線(インボリュート曲線・伸開線))などを使う場合や、半径の大きな曲線を直線との間に入れる場合などでは、直線と繋がる部分で曲率に段違いが発生するので、そのような方法に比べれば、直線との接続部分が角折れになることはあまり心配しないでよいでしょう。
