三次放物線(JP)
計算のことはさておき、三次放物線(JP)について簡単に紹介します。
三次放物線(JP)とは
曲率が完全に直線で逓減するクロソイド曲線の代わりに使われる三次放物線を日本で独自に改良した曲線です。日本では特に断りなく三次放物線と表記しますが、ここでは区別の為に三次放物線(JP)と表記します。
三次放物線(JP)は緩和曲線の始点と終点で曲率に角折れが発生する直線逓減で、曲がることのできる角度は90°未満です。軌道中心の道のりをパラメーターにする曲線です。
三次放物線(JP)の値 - 緩和曲線自体
円曲線の半径を \(R\) 、緩和曲線始点から測った軌道中心の長さを\(l\)、緩和曲線全長を \(L\) と表記します。曲率を\( \kappa \)と書きます。緩和曲線の途中の曲がった角度を \( \theta \) 、緩和曲線全長で曲がる角度を \( \Theta \) と表記します。 三次放物線(JP)の定義は
\[ \begin{align} y &= al^{3} \\ \end{align} \]です。\(y\)の微分は以下になります。、
\[ \begin{align} \frac{dy}{dl} &= 3al^{2} \\ \frac{d^{2}y}{dl^{2}} &= 6al \\ \end{align} \]パラメータである長さ\(l\)は速さ1にとることができるので、
\[ \begin{align} v &= \left|\left( \frac{dx}{dl} \right)^{2} + \left( \frac{dy}{dl} \right)^{2} \right|^{\frac{1}{2}} = 1 \\ \end{align} \]とできます。これから\(x\)の微分は以下のように書けます。
\[ \begin{align} \frac{dx}{dl} &=\sqrt{1-\left( \frac{dy}{dl} \right)^{2} } \\ &= \sqrt{1-(3al^{2})^{2}}\\ \end{align} \]ただし、
\[ \begin{align} \left|\frac{dy}{dl}\right| = \left|3al^{2}\right| \le 1 \tag{1}\\ \end{align} \]です。\(x\)の2階微分は以下になります。
\[ \begin{align} \frac{d^{2}x}{dl^{2}} &= - \frac{-18a^{2}l^{3}}{\sqrt{1-9a^{2}l^{4}}} \\ \end{align} \]ここまでの結果から曲率を計算すると、
\[ \begin{align} \kappa &= \frac{\left| \frac{dx}{dl} \frac{d^{2}y}{dl^{2}} - \frac{dy}{dl} \frac{d^{2}x}{dl^{2}} \right|}{|v|^{3}} \\ &= \frac{6al}{\sqrt{1-9a^{2}l^{4}}} \\ \end{align} \]となります。\(\frac{d\kappa}{dl}\)は
\[ \begin{align} \frac{d\kappa}{dl} &= \frac{6a(1+9a^2l^4)}{(1-9a^2l^4)^{\frac{3}{2}}} \gt 0 \\ \end{align} \]であり、曲率\(\kappa\)は単調増加します。緩和曲線で曲がれる角度は90°に到達しません。
円曲線の半径が \(R\)、緩和曲線長が \(L\) のとき、\(R\) と \(a\) は以下の式を満たします。
\[\begin{align} \frac{1}{R} = {\kappa}_{L} &= \frac{6aL}{\sqrt{1-9a^{2}L^{4}}} \\ \end{align}\]ここから両辺を2乗して変形し、
\[\begin{align} 1-9a^{2}L^{4} = 36a^{2}L^{2}R^{2}\\ (36R^{2} +9L^{2})L^{2}a^{2} - 1 = 0\\ 9(4R^{2} +L^{2})L^{2}\left(a^{2} - \frac{1}{9(4R^{2} +L^{2})L^{2}}\right) = 0\\ \end{align}\]となり、求めたい\(a (\ge 0) \)は、
\[\begin{align} a &= \frac{1}{3L\sqrt{4R^{2}+L^{2}}} \tag{2}\\ &= \frac{1}{6LR}\frac{1}{ \sqrt{1+\frac{L^{2}}{4R^{2}} } } \\ \end{align}\]となります。またこの表式を(1)️式に代入すると、恒等的に成り立つことがわかります。
緩和曲線で曲がる角度\(\theta\)は、
\[\begin{align} \theta &= \int_{0}^{l} \kappa dl \\ &= \int_{0}^{l} \frac{6al}{\sqrt{1-9a^{2}l^{4}}} dl\\ \end{align}\]\(3al^2 = \sin k\)と置くことで、
\[\begin{align} \theta &= \int_{0}^{\mathrm{Sin}^{-1}3al^{2}} \frac{2\sqrt{3a\sin k}}{\sqrt{1-\sin^{2}k}} \frac{dl}{dk}dk\\ &= \int_{0}^{\mathrm{Sin}^{-1}3al^{2}} \frac{2\sqrt{3a\sin k}}{\cos k} \frac{dl}{dk}dk\\ \end{align}\]\(\frac{dl}{dk}\)は、
\[\begin{align} \frac{dl}{dk} &= \frac{d}{dk} \sqrt{\frac{\sin k}{3a}} \\ &= \frac{\cos k}{2\sqrt{3a\sin k}} \end{align}\]と書けるので、被積分関数は1となり、
\[\begin{align} \theta &= \int_{0}^{\mathrm{Sin}^{-1}3al^{2}} dk\\ &= \left[ k \right]_{0}^{\mathrm{Sin}^{-1}3al^{2}} \\ &= \mathrm{Sin}^{-1}3al^{2}\\ \end{align}\]となります。これを以下のように変形して、
\[\begin{align} \sin\theta &= 3al^{2}\\ \end{align}\]と書けるので、\(a\)の表式(2)と組み合わせることで緩和曲線全体で曲がる角度\(\Theta\)は、
\[\begin{align} \sin\Theta &= \frac{L}{\sqrt{4R^{2}+L^{2}}} \\ \cos\Theta&= \frac{2R}{\sqrt{4R^{2}+L^{2}}} \\ \tan\Theta&= \frac{L}{2R} \\ \end{align}\]と書けます。これらを使って、(2)式を書き換えると、
\[ a = \frac{\cos\Theta}{12R^2\tan\Theta} = \frac{\cos^{2}\Theta}{12R^2\sin\Theta} \]となり、\(a\)を\(R\)と\(\Theta\)だけを使って書くことができます。また別の表記として、
\[ a = \frac{1}{6LR}\frac{1}{\sqrt{1+\tan^2 \Theta}} =\frac{\cos\Theta}{6LR} \]となります。また簡易計算としては、\(\Theta \ll 1\)とみなすことで、
\[ a \sim \frac{1}{6LR} \]となります。
なお\(x\)は、
\[\begin{align} x &= \int_{0}^{l} \frac{dx}{dl} dl\\ &= \int_{0}^{l} \sqrt{1-9a^2l^4}dl\\ \end{align}\]となり解析的には計算できません。ルートを展開して、
\[\begin{align} x &= - \sum_{n=0}^{\infty} \int_{0}^{l} \frac{(2n-3)!!}{2^n n!}(9a^2l^4)^n \, dl\\ &= - \sum_{n=0}^{\infty} \left[ \frac{(2n-3)!! \, 9^n a^{2n}}{2^n n! (4n+1)}l^{4n+1} \right]_0^l \\ &= - \sum_{n=0}^{\infty} \frac{(2n-3)!! \, 9^n a^{2n}}{(2n)!!\, (4n+1)}l^{4n+1} \\ &= - \sum_{n=0}^{\infty} \frac{(2n-3)!! }{(2n)!!\, (4n+1) } \frac{ l^{4n+1}}{ L^{2n}(4R^2+L^2)^n} \\ &= l \left[ 1 - \frac{1}{10}\frac{l^4}{L^2(4R^2+L^2)} - \frac{1}{72}\frac{ l^8}{ L^4(4R^2+L^2)^2} - \frac{1}{208}\frac{ l^{12}}{ L^6(4R^2+L^2)^3 } - ... \right] \\ \end{align}\]となります。なおマイナスの二重階乗の定義は、
\[\begin{align} (-1)!! &= 1 \\ (-3)!! &= -1 \\ \end{align}\]を採用します。
\(\kappa \, - \, l\)のグラフは、以下のようなグラフになります。
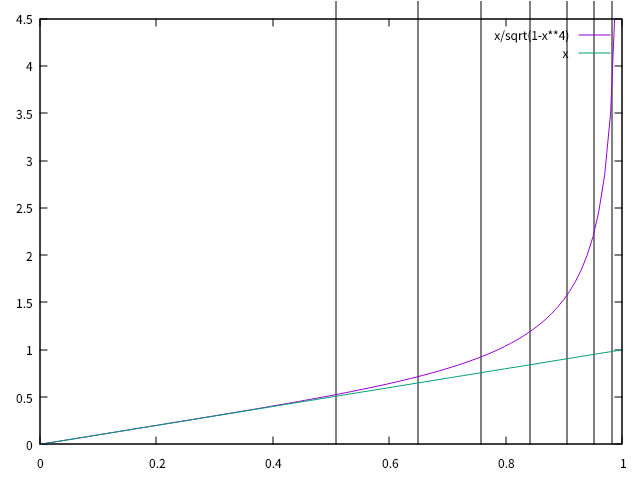
曲率の勾配の最大値がどのように変化するか調べます。曲率の勾配の最大値は円曲線と繋がる点なので、
\[ \begin{align} \left.\frac{d\kappa}{dl}\right|_{l=L} &= \frac{6a(1+9a^2L^4)}{(1-9a^2L^4)^{\frac{3}{2}}} \tag{3}\\ \end{align} \]\(a\)は\(L\)に依存するので、(3)に(2)を代入して、
\[ \begin{align} \left.\frac{d\kappa}{dl}\right|_{l=L} &= \frac{6\left(1+\frac{9L^4}{9L^2(4R^2+L^2)}\right)}{3L\sqrt{4R^2+L^2}\left(1-\frac{9L^4}{9L^2(4R^2+L^2)}\right)^{\frac{3}{2}}} \\ &= \frac{2\left(1+\frac{L^2}{4R^2+L^2}\right)}{L\sqrt{4R^2+L^2}\left(1-\frac{L^2}{4R^2+L^2}\right)^{\frac{3}{2}}} \\ &= \frac{2\frac{4R^2+L^2+L^2}{4R^2+L^2}}{L\sqrt{4R^2+L^2}\left(\frac{4R^2+L^2-L^2}{4R^2+L^2}\right)^{\frac{3}{2}}} \\ &= \frac{2(4R^2+2L^2)\sqrt{4R^2+L^2}}{L\sqrt{4R^2+L^2}\left(4R^2\right)^{\frac{3}{2}}} \\ &= \frac{2(4R^2+2L^2)}{8LR^3} \\ &= \frac{2R^2+L^2}{2LR^3} \\ \end{align} \]\(L\)が小さいときは、
\[ \begin{align} \frac{1}{LR} \\ \end{align} \]に近くなり、\(L\)が大きなときは、
\[ \begin{align} \frac{L}{2R^3} \\ \end{align} \]に近くなります。\(L\)が小さなときは減少関数で、ある値で極小値をとり増加に転じることがわかります。
\(\frac{L}{R}\)を使って書きなおすと、
\[ \begin{align} \left.\frac{d\kappa}{dl}\right|_{l=L} &= \frac{1}{2R^2}\frac{2+\frac{L^2}{R^2}}{\frac{L}{R}} \\ \end{align} \]\(\left.\frac{d\kappa}{dl}\right|_{l=L}\cdot R^2 \, - \, \frac{L}{R}\)のグラフは、以下のようなグラフになります。
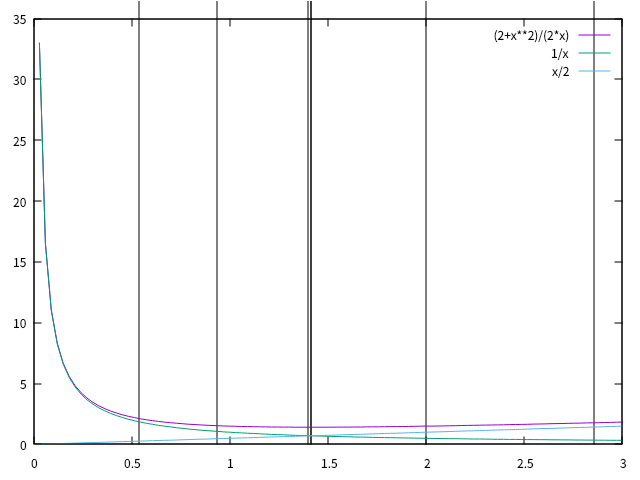
極小値を求めるために、\(L\)微分を計算します
\[ \begin{align} \frac{d}{dL}\left(\left.\frac{d\kappa}{dl}\right|_{l=L}\right) &= \frac{1}{2R^3}\frac{1}{L^2}\big( 2L \cdot L - (2R^2+L^2)\cdot 1 \big) \\ &= \frac{L^2-2R^2}{2R^3L^2} \\ &= \frac{1}{2R^3}\frac{\frac{L^2}{R^2}-2}{\frac{L^2}{R^2}} \\ \end{align} \]\( \frac{d}{dL}\left(\left.\frac{d\kappa}{dl}\right|_{l=L}\right) = 0 \)となるのは、
\[ L^2-2R^2 = 0 \]のときです。このとき、
\[ \begin{align} L = \sqrt{2}R \tag{4}\\ \frac{L}{R} = \sqrt{2} \sim 1.414...\\ \end{align} \]です。このときの角度\(\Theta\)は、
\[ \begin{align} \tan\Theta = \frac{L}{2R} = \frac{1}{\sqrt{2}} \\ \Theta \sim 35.264...\mathrm{[deg]} \\ \end{align} \]一方、\(\frac{d\kappa}{dl}\)は
\[ \begin{align} \frac{d\kappa}{dl} &= \frac{6a(1+9a^2l^4)}{(1-9a^2l^4)^{\frac{3}{2}}} \\ \end{align} \]で、曲率の勾配が最小値をとるのは\(l=0\)のときで、
\[ \begin{align} \left.\frac{d\kappa}{dl}\right|_{l=0} &= 6a \\ \end{align} \]緩和曲線終点の曲率の勾配が緩和曲線始点の何倍になるかは、
\[ \begin{align} \frac{\left.\frac{d\kappa}{dl}\right|_{l=L}}{\left.\frac{d\kappa}{dl}\right|_{l=0}} &= \frac{(1+9a^2L^4)}{(1-9a^2L^4)^{\frac{3}{2}}} \\ &= \frac{1+\frac{9L^4}{9L^2(4R^2+L^2)}}{\left(1-\frac{9L^4}{9L^2(4R^2+L^2)}\right)^{\frac{3}{2}}} \\ &= \frac{1+\frac{L^2}{4R^2+L^2}}{\left(1-\frac{L^2}{4R^2+L^2}\right)^{\frac{3}{2}}} \\ &= \frac{\frac{4R^2+L^2+L^2}{4R^2+L^2}}{\left(\frac{4R^2+L^2-L^2}{4R^2+L^2}\right)^{\frac{3}{2}}} \\ &= \frac{(4R^2+2L^2)\sqrt{{4R^2+L^2}}}{\left({4R^2}\right)^{\frac{3}{2}}} \\ &= \frac{(2R^2+L^2)\sqrt{{4R^2+L^2}}}{4R^3} \\ &= \frac{1}{4}\left(2+\frac{L^2}{R^2}\right)\sqrt{4+\frac{L^2}{R^2}} \\ \end{align} \]と表せます。
緩和曲線終点の曲率の勾配が極小値をとる\(L\)のとき、この値は(4)を代入することで、
\[ \begin{align} \frac{\left.\frac{d\kappa}{dl}\right|_{l=L}}{\left.\frac{d\kappa}{dl}\right|_{l=0}} &= \frac{(2R^2+2R^2)\sqrt{{4R^2+2R^2}}}{4R^3} \\ &= \frac{4\sqrt{6}}{4} \\ &= \sqrt{6} \sim 2.449...\\ \end{align} \]と表せます。緩和曲線として意味のある範囲では、曲率の勾配の緩和曲線終点と緩和曲線始点の比は、最大で\(\sqrt{6}=2.449...\)となります。
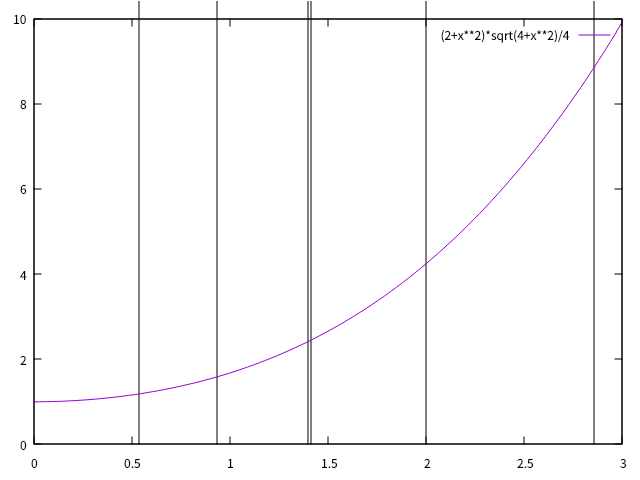
緩和曲線で曲がることのできる角度の範囲は三次放物線よりは大きくなりますが、約35.264°と制限があります。模型で使いやすい角度の範囲には対応できるようです。
