サイン半波長逓減曲線(模型向けの代用)
模型用に改変したサイン半波長逓減曲線を紹介します。
曲率が厳密にサイン波の谷から山までの半波長で逓減するのではなく、それに似た形状の曲線として模型向けの代用としての曲線について記載します。直線逓減における、クロソイド曲線に対する三次放物線に相当する曲線の一種です。ここではサイン半波長逓減曲線(模型向けの代用)と表記します。
模型向けの代用方法
緩和曲線で曲がる角度が大きくなると、緩和曲線と円曲線のつなぎ目までの距離を計算することが大変になるので、緩和曲線と円曲線の境界に接する線を \(x\) 軸とする方法が、模型では計算が便利です。
実物では直線からそのまま真っすぐ伸ばした \(x\)軸を使って
\[ y = a x^2 - A \frac{1-\cos kx}{2} \]とするようですが、以下のように円曲線と緩和曲線の境界の接線を \(x\)軸とする方が模型には計算が容易になります。
\[ y = a \left( x - \frac{\pi}{k} \right)^2 - A \frac{1-\cos kx}{2} \]ただし、緩和曲線長\(X\)は、
\[ X = \frac{\pi}{k} \]\(y'\)を正にとるために符号を変え、原点から伸びる曲線とするために係数を加えると、
\[ y = -a \left( x - \frac{\pi}{k} \right)^2 + b + A \frac{1-\cos kx}{2} \]ただし、 \(b\)は、
\[ b = a \left( \frac{\pi}{k} \right)^2 \]\(y'\)は、
\[ y' = -2a \left( x - \frac{\pi}{k} \right) +\frac{Ak}{2}\sin kx \]\(y''\)は、
\[ y'' = -2a + \frac{Ak^2}{2}\cos kx \]\(x=0\)で\(y''=0\)なので、\(2a=\frac{Ak^2}{2}\)となり、
\[ y'' = -\frac{Ak^2}{2}(1-\cos kx ) \]\(\kappa\)は、
\[ \kappa = \frac{y''}{|v|^3} \]ただし\(|v|\)は、
\[ |v| = \sqrt{1+(y')^2} \]\(y'\)は、\(x\)が緩和曲線長\(X\)のとき、
\[ y'|_{x=X} = 0 \]なので、
\[ \frac{1}{R} = -\kappa_{X} = Ak^2 \]角度ベースの値 - 緩和曲線自体
円曲線の半径を \(R\) 、緩和曲線で曲がる角度を \(\Theta\) とすると、緩和曲線 \(y = A \frac{1-\cos kx }{2} - a \left( x - \frac{\pi}{k} \right)^2 + b\) の係数 \(A\) と \(k\) , \(a\) , \(b\) は、以下のようになります。
\[\begin{align} %y &= A \frac{1-\cos kx}{2} - a \left( x - \frac{\pi}{k} \right)^2 + b \\ a &= \frac{Ak^2}{4} = \frac{1}{4R} \\ b &= a \left(\frac{\pi}{k}\right)^2 = \frac{A\pi^2}{4} \\ \end{align}\] \[\begin{align} \tan\Theta &= y'|_{x=0} = \frac{Ak\pi}{2} \\ \end{align}\]変形して、
\[\begin{align} Ak &= \frac{2\tan\Theta}{\pi} \tag{1}\\ \end{align}\]これを、
\[\begin{align} Ak^2 &= \frac{1}{R} \\ \end{align}\]で割ることで、
\[\begin{align} \frac{1}{k} &= \frac{2R \tan\Theta}{\pi} \tag{2}\\ \end{align}\]となります。(1)式にこれをかけて、
\[\begin{align} A &= \frac{4R\tan^2\Theta}{\pi^2} \tag{3}\\ \end{align}\](2)式を変形して、
\[\begin{align} R &= \frac{\pi}{2k \tan\Theta} \tag{4}\\ \end{align}\]また、
\[\begin{align} X &=\frac{\pi}{k}\\ \end{align}\]を、(4)式を変形してたものに代入することで、
\[\begin{align} \tan\Theta &= \frac{\pi}{2Rk} = \frac{X}{2R} \\ \end{align}\]これを(3)式に代入して、
\[\begin{align} A &= \frac{X^2}{\pi^2R} \\ \end{align}\]これらを使って\(y\)を書くと、
\[\begin{align} y &= \frac{X^2}{2\pi^2R} \left( 1-\cos \frac{x}{X}\pi \right) - \frac{1}{4R} \left( x - X \right)^2 + \frac{X^2}{4R} \\ &= \frac{2R\tan^2\Theta}{\pi^2} \left( 1-\cos \frac{\pi}{2R\tan\Theta}x \right) - \frac{1}{4R} \left( x - 2R\tan\Theta \right)^2 + R\tan^2\Theta \\ \end{align}\]\(y'\) と \(y''\) は以下のように書くことができます。
\[\begin{align} y'' &= -\frac{1}{R} \frac{1-\cos kx }{2} \\ y' &= -\frac{Ak}{2} \left( kx - \pi \right) +\frac{Ak}{2}\sin kx \\ &= \frac{\tan\Theta}{\pi} \left( \pi -kx +\sin kx \right)\\ \end{align}\]これらを使って\(\kappa\) を書くと、
\[\begin{align} \kappa &= -\frac{1}{2R} \frac{1-\cos kx } { \left[ 1 + \left(\frac{\tan\Theta}{\pi}\right)^2 \left( \pi -kx +\sin kx \right)^2 \right]^\frac{3}{2} }\\ \end{align}\]となり、\(\kappa\)が\(\Theta\)にどのように依存するか書くことができました。
\(\Theta\)を変えながら\(\kappa\)のグラフを描くと以下のようになります。
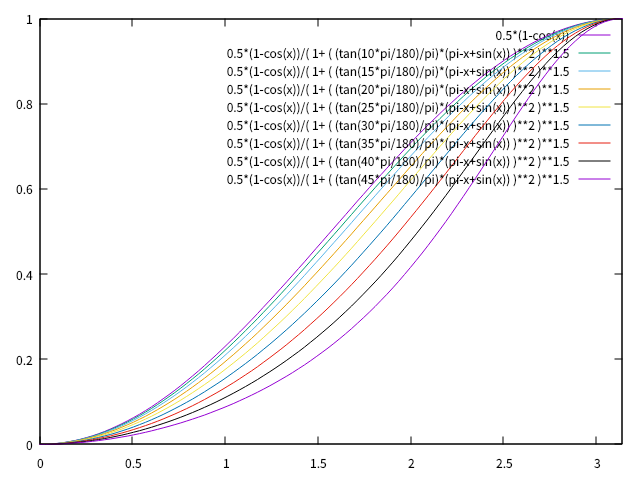
なお、曲率のグラフは横軸がx軸であることに注意してください。サイン半波長逓減曲線(模型向けの代用)の形状とx軸とy軸は、下のグラフの横軸と縦軸のようになります。曲率のグラフの横軸を実際の緩和曲線の長さとした場合、上のグラフの横軸を、左側に行くにつれて左側に引き延ばしていくような感じになります。なお\(\Theta\)の値の違いによる右下に膨れる形状について、実際の緩和曲線の経路でグラフを描きなおしても改善に大きく寄与することはないでしょう。
中間緩和曲線
\(y''\) から導出しなおすことで中間緩和曲線に適用することができます。
\[\begin{align} y'' &=- \frac{1}{R_1} -\left( \frac{1}{R_2} - \frac{1}{R_1}\right) \frac{1-\cos kx }{2} \\ &=- \frac{1}{2} \left(\frac{1}{R_2} + \frac{1}{R_1} \right) + \frac{1}{2} \left( \frac{1}{R_2} - \frac{1}{R_1}\right) \cos kx \\ y' &=- \frac{1}{2} \left(\frac{1}{R_2} + \frac{1}{R_1} \right) \left(x - \frac{\pi}{k} \right) + \frac{1}{2k} \left( \frac{1}{R_2} - \frac{1}{R_1}\right) \sin kx \\ y &=- \frac{1}{4} \left(\frac{1}{R_2} + \frac{1}{R_1} \right) \left[\left(x - \frac{\pi}{k} \right)^2 - \left(\frac{\pi}{k}\right)^2 \right] - \frac{1}{2k^2} \left( \frac{1}{R_2} - \frac{1}{R_1}\right) \cos kx \\ &=- \frac{1}{4} \left(\frac{1}{R_2} + \frac{1}{R_1} \right) \left[\left(x - X \right)^2 -X^2 \right] - \frac{X^2}{2\pi^2} \left( \frac{1}{R_2} - \frac{1}{R_1}\right) \cos \frac{x}{X}\pi \\ \end{align}\]\(\tan\Theta\)は、
\[\begin{align} \tan\Theta &= y'|_{x=0} = \frac{\pi}{2k} \left(\frac{1}{R_2} + \frac{1}{R_1} \right) \\ \end{align}\]から変形して、
\[\begin{align} k\ &= \frac{\pi}{2\tan\Theta} \left(\frac{1}{R_2} + \frac{1}{R_1} \right) \\ \end{align}\]また\(\tan\Theta\)を\(X\)を使って書くと、
\[\begin{align} \tan\Theta &= \frac{X}{2} \left(\frac{1}{R_2} + \frac{1}{R_1} \right) \\ \end{align}\]となり、\(X\)は、
\[\begin{align} X &= \frac{2\tan\Theta}{\frac{1}{R_2} + \frac{1}{R_1} } \\ \end{align}\]これらを使って書き換えると、
\[\begin{align} y &=- \frac{1}{4} \left(\frac{1}{R_2} + \frac{1}{R_1} \right) \left[\left(x - \frac{2\tan\Theta}{\frac{1}{R_2} + \frac{1}{R_1} } \right)^2 -\left(\frac{2\tan\Theta}{\frac{1}{R_2} + \frac{1}{R_1} }\right)^2 \right] \\ & \quad\quad\quad - \frac{2\tan^2\Theta}{\pi^2\left(\frac{1}{R_2} + \frac{1}{R_1} \right)^2} \left( \frac{1}{R_2} - \frac{1}{R_1}\right) \cos \frac{\pi \left(\frac{1}{R_2} + \frac{1}{R_1} \right) }{2\tan\Theta}x \\ &=- \frac{1}{4} \left(\frac{1}{R_2} + \frac{1}{R_1} \right) \left(x - \frac{2\tan\Theta}{\frac{1}{R_2} + \frac{1}{R_1} } \right)^2 + \frac{\tan^2\Theta}{\frac{1}{R_2} + \frac{1}{R_1} } \\ & \quad\quad\quad - \frac{2\tan^2\Theta}{\pi^2} \frac{ \frac{1}{R_2} - \frac{1}{R_1}}{\left(\frac{1}{R_2} + \frac{1}{R_1} \right)^2} \cos \frac{\pi }{2\tan\Theta}\left(\frac{1}{R_2} + \frac{1}{R_1} \right) x \\ \end{align}\]