サイン半波長逓減曲線(代用)
計算のことはさておき、サイン半波長逓減曲線(代用)の各種数値を紹介します。
サイン半波長逓減曲線(代用)とは
曲率が厳密にサイン波の谷から山までの半波長で逓減するのではなく、それに似た形状の曲線として実物で代用される曲線について記載します。直線逓減における、クロソイド曲線に対する三次放物線に相当する曲線です。ここではサイン半波長逓減曲線(代用)と表記します。
曲がる角度が小さい場合であれば、緩和曲線終点で曲率に段違いができても問題ないだろうとの判断で使用される曲線のようです。模型のように大きな角度で曲がる場合には使用できません。実物でも3度台までの使用のようです。
角度ベースの値 - 緩和曲線自体
曲率が厳密にサイン波の谷から山までとなる曲線は、積分が困難なため、曲率がサイン波の谷から山までに似た形状になる曲線を考えます。
\(x\)で書かれた曲線\(y\)の曲率\(\kappa\)は以下のように書けます。
\[ \kappa = \frac{y''}{|v|^3} \]ただし\(|v|\)は、
\[ |v| = \sqrt{ 1 + (y')^2} \]です。角度\(\theta\)は\(y\)の微分を使って、
\[ \tan\theta = y' \]と書けることから、\(|v|\)は、
\[ |v| = \sqrt{ 1 + \tan^2\theta } = \frac{1}{\cos\theta} \]これらを使って\(\kappa\)を書き換えると、
\[ \kappa = y'' \, \cos^3\theta \]三次放物線では曲率ではなく\(y''\)が直線になっているように、\(y''\)がサイン波の谷から山までの形状を考えます。
緩和曲線長を\(X\)と書き、この時の\(\theta\)を\(\Theta\)と書くと、
\[ \left.\kappa_X = y''\right|_{x=X} \, \cos^3\Theta \]円曲線の半径を\(R\)と書いて、
\[ \frac{1}{R} = \left.y''\right|_{x=X} \]とすると、
\[ \kappa_X = \frac{1}{R}\cos^3\theta \]緩和曲線終点の曲率が円曲線の曲率\(\frac{1}{R}\)に到達していませんが、曲線逓減であれば曲率に小さな段違いがあっても緩和曲線として使用できると思われるので、\(\cos\Theta \sim 1\)であれば緩和曲線として使用できるようです。
\(y''\)がサインの谷から山までの半波長の場合、以下のように書くことができます。
\[ y'' = Ak^2 \frac{1-\cos kx}{2} \]ただし、
\[ 0 \leq x \leq \frac{\pi}{k} \] \[ Ak^2 = \frac{1}{R} \tag{1} \]\(y'\)は、
\[ y' = \int y'' dx = \frac{Ak^2}{2} x - \frac{Ak}{2} \sin kx \]と書けます。
\[\begin{align} \kappa' &= y''' \, \cos^3\theta - 3y'' \theta' \, \cos^2\theta \sin\theta \\ &= (y''' \, \cos\theta - 3y'' \theta' \, \sin\theta ) \cos^2\theta \\ \end{align} \]と書けます。\(\kappa' = 0\)となる\(x\)で\(\kappa\)は極大値を取ります。
\(\cos\theta \rightarrow 1\) のとき、 \(x \rightarrow \frac{\pi}{k}\) で\(\kappa\) は極大になります。 \(\cos\theta \lt 1\)のとき、\(\kappa\)が極大となる\(x\)は\(x \lt \frac{\pi}{k}\) となります。
\(y\)は、
\[ y = \int y' dx = \frac{Ak^2}{4} x^2 - \frac{A}{2} (1-\cos kx) \]となります。
緩和曲線長\(X\)は、
\[ X = \frac{\pi}{k} \tag{2} \]から、
\[ k = \frac{\pi}{X} \tag{3} \](1)を変形して(3)を代入して、
\[ A = \frac{1}{k^2R} = \frac{X^2}{\pi^2 R} \tag{4} \]曲がった角度\(\theta\)は以下のように書くことができます。
\[ \tan\theta = y' = \frac{Ak^2}{2} x - \frac{Ak}{2} \sin kx \]\(\Theta\)は(1)を使って変形することで以下のように書くことができます。
\[\begin{align} \tan\Theta = \frac{Ak^2}{2}X = \frac{X}{2R} \tag{5}\\ \end{align}\]これから、
\[\begin{align} X=2R\tan\Theta\\ \end{align}\]と変形して(4)に代入して、
\[\begin{align} A &= \frac{4R}{\pi^2} \tan^2\Theta \tag{6}\\ \end{align}\](5)式を変形して(2)を代入して、
\[\begin{align} Ak^2 &= \frac{2\tan\Theta}{X} = \frac{2k\tan\Theta}{\pi}\\ \end{align}\]両辺を\(k\)で割って、
\[\begin{align} Ak &= \frac{2\tan\Theta}{\pi} \\ \end{align}\]変形して(6)を代入して、
\[\begin{align} \frac{1}{k} &= \frac{\pi A}{2\tan\Theta} = \frac{2R}{\pi} \tan\Theta \\ \end{align}\]と書けます。(5)式を使って\(\tan\Theta\)を書き換えると、
\[\begin{align} % R &= \frac{1}{4k\tan\Theta} \\ Ak &= \frac{2\tan\Theta}{\pi} = \frac{X}{\pi R} \\ A &= \frac{4R}{\pi^2} \tan^2\Theta = \frac{X^2}{\pi^2R} \\ \frac{1}{k} &= \frac{2R}{\pi} \tan\Theta = \frac{X}{\pi} \\ \end{align}\]これらを使って係数を書き換えると、\(\Theta\)を使った表式は、
\[\begin{align} y %&= \frac{1}{4R} x^2 - \frac{4R}{\pi}\tan^2\Theta \sin^2 \frac{kx}{2} \\ &= \frac{1}{4R} x^2 - \frac{2R\tan^2\Theta}{\pi^2} \left(1 - \cos \frac{\pi}{2R\tan\Theta} x \right) \\ \end{align}\]となります。\(X\)を使った表式は、
\[\begin{align} y %&= \frac{1}{4R} x^2 - \frac{X^2}{\pi^2R} \sin^2 \frac{\pi}{4X}x \\ &= \frac{1}{4R} x^2 - \frac{X^2}{2\pi^2R} \left( 1 - \cos \frac{\pi}{X}x \right) \\ \end{align}\]また\(y'\)と\(y''\)は以下のように書くことができます。
\[\begin{align} y'' &= \frac{1}{R} \frac{1-\cos kx}{2}\\ \end{align}\] \[\begin{align} y' &=\frac{Ak}{2} (kx - \sin kx ) \\ &=\frac{\tan\Theta}{\pi} (kx - \sin kx ) \\ \end{align}\]これらを使って\(\kappa\)を書くと、
\[\begin{align} \kappa %&= \frac{\frac{1}{R} \frac{1-\cos kx}{2}}{ \left[ 1 - \left( \frac{\tan\Theta}{\pi} (kx - \sin kx ) \right)^2 \right]^{\frac{3}{2}} }\\ &= \frac{1}{2R} \frac{1-\cos kx}{ \left[ 1 + \left(\frac{\tan\Theta}{\pi}\right)^2 (kx - \sin kx )^2 \right]^{\frac{3}{2}} }\\ \end{align}\]\(\kappa'\)は緩和曲線全体で曲がる角度\(\Theta\)に依存することがわかります。
\(\Theta\)を変えながら\(\kappa'\)がどのような形状になるか示したグラフが以下です。
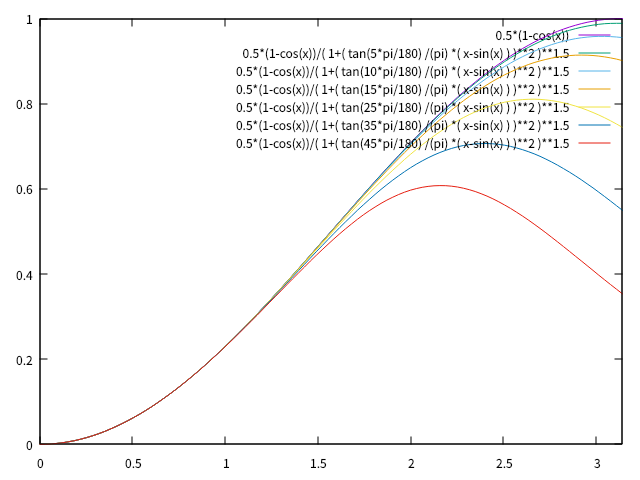
グラフの右上四分の一を拡大したのが以下のグラフです。
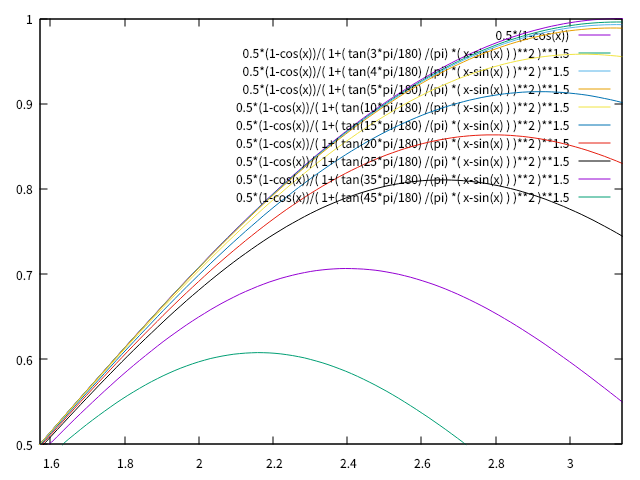
|v| が X で厳密に 1 になるようにすることで、鉄道模型向けに少し計算しやすくする方法(模型向けの代用)も紹介してますが、その方法を利用した場合では、角度が大きくなるとサイン半波長から大きく曲率の形状が外れるようになっています。
中間緩和曲線
\(y''\)から導出しなおすことで中間緩和曲線に適用することができます。\(R_1 \gt R_2\)のとき、\(y''\)は、
\[\begin{align} y'' &= \frac{1}{R_1} + \left(\frac{1}{R_2} - \frac{1}{R_1}\right) \frac{1-\cos kx}{2} \\ &= \frac{1}{2} \left(\frac{1}{R_2} + \frac{1}{R_1}\right) - \frac{1}{2} \left(\frac{1}{R_2} - \frac{1}{R_1}\right) \cos kx \\ \end{align}\]\(y'\)は、
\[\begin{align} y' &= \frac{1}{2} \left(\frac{1}{R_2} + \frac{1}{R_1}\right) x - \frac{1}{2k} \left(\frac{1}{R_2} - \frac{1}{R_1}\right) \sin kx \\ \end{align}\]\(y\)は、
\[\begin{align} y &= \frac{1}{4} \left(\frac{1}{R_2} + \frac{1}{R_1}\right) x^2 - \frac{1}{2k^2} \left(\frac{1}{R_2} - \frac{1}{R_1}\right) \left( 1 - \cos kx \right)\\ &= \frac{1}{4} \left(\frac{1}{R_2} + \frac{1}{R_1}\right) x^2 - \frac{X^2}{2\pi^2} \left(\frac{1}{R_2} - \frac{1}{R_1}\right) \left( 1 - \cos \frac{x}{X}\pi \right)\\ &= \frac{R_1 + R_2}{4R_1R_2} x^2 - \frac{X^2}{2\pi^2} \frac{R_1-R_2}{R_1R_2} \left( 1 - \cos \frac{x}{X}\pi \right)\\ \end{align}\]\(\tan\theta=y'\)なので、、
\[\begin{align} \tan\Theta &= \frac{X}{2} \left(\frac{1}{R_2} + \frac{1}{R_1}\right) = \frac{\pi}{2k} \left(\frac{1}{R_2} + \frac{1}{R_1}\right) \\ &= \frac{2R_2+R_1}{R_2R_1} X \\ \end{align}\]\(\tan\Theta\)を使って\(y\)を書くと、
\[\begin{align} y &= \frac{1}{4} \left(\frac{1}{R_2} + \frac{1}{R_1}\right) x^2 - \frac{2\tan^2\Theta}{\pi^2 } \frac{\frac{1}{R_2} - \frac{1}{R_1}}{\left(\frac{1}{R_2} + \frac{1}{R_1}\right)^2} \left( 1 - \cos \frac{\pi}{2\tan\Theta} \left(\frac{1}{R_2} + \frac{1}{R_1}\right) x \right)\\ &= \frac{R_1+R_2}{4R_1R_2} x^2 - \frac{2 \tan^2\Theta}{\pi^2}\frac{R_1R_2(R_1-R_2)}{\left(R_1 +R_2\right)^2 } \left( 1 - \cos \frac{\pi}{2\tan\Theta} \frac{R_1+R_2}{R_1R_2} x \right)\\ \end{align}\]なお、曲率に段差が発生するのは半径の小さな\(R_2\)の側だけになります。
